Audio Artistry Inc., Corte Madera, CA 94925, USA
May 1998

(Presented at the AES 105th Convention, 1998 September 26-29, San Francisco, California, #4786)

ABSTRACT

In acoustically small rooms the naturalness of low frequency reproduction may differ between dipolar and monopolar radiating woofers. The coupling of the two types of sources to the modal structure of the room is investigated using steady-state frequency response, cumulative spectral decay, energy-time curve, modulation transfer function and tone burst response. When sets of shaped tone bursts are used for measurement and listening, both frequency and time domain attributes are brought to light which point to the perceived differences.

Listening to two channel stereo or 5.1 channel home theater sound under domestic conditions usually takes place in rooms that are acoustically small over part of the audio spectrum. At low frequencies where the wavelength of sound is as long, even a fairly large room with a floor plan of 7.63 m by 4.88 m (25 ft by 16 ft) and a 2.75 m (9 ft) height is small when compared to a 20 Hz wavelength of 17.2 m (56 ft). Above 200 Hz and 1.72 m (5.6 ft) wavelength, though, most domestic rooms enter a wavelength region where they must be considered acoustically large. The bass frequency range from 15 Hz to 150 Hz, thus, covers a unique chapter in room acoustics: from the region where no standing waves can exist, to the first few room resonances, to ever increasing numbers of modes towards higher frequencies. It is not surprising then, that bass reproduction varies widely between rooms of different sizes, proportions and construction.

A number of listeners have observed that the quality of bass is different whether reproduced by a monopolar, i.e. omnidirectional woofer, or a dipolar, i.e. directional, figure-of-eight radiating woofer. The bass "boom" often heard with an omnidirectional source is less pronounced with a directional one. Furthermore, low frequency sonic detail can be presented with greater resolution and life likeness from a dipolar woofer. While the "boom" may enhance the impact of movie sound effects in some instances, it is undesirable for accurate reproduction of musical instruments and voices. It must be acknowledged, though, that upon first exposure to bass from a dipole woofer some listeners prefer the generic loudspeaker bass, possibly because their primary sonic reference is amplified sound and other box speakers. However, after a period of acclimatization the preference changes when accompanied by attention and reference to acoustic instrument sounds and voices.

The different behavior of monopole and dipole sources in a room has been recognized and investigated previously [1, 2, 3]. This study is an attempt to carry that work further and to find objective measures that explain the subjectively observed differences. The work is focused on low frequency reproduction only. At higher frequencies where a room is acoustically large, the primary benefits of a dipolar source with well behaved polar response are: a smooth off-axis frequency response, a lower level of the reverberant sound field, a spectral balance of the reverberant sound field equivalent to that of the on-axis sound pressure and the absence of box coloration due to an open baffle design [3]. All of this results in a sound that is more open and life like and less influenced by speaker placement and the room. The benefits of a dipolar source for low frequencies are not as obvious.

The steady-state sound pressure distribution in a closed, rectangular rigid room may be thought of as being formed by the total of standing waves or room modes that fit the boundary condition, namely that the normal component of the particle velocity must vanish at the surface of the walls. The eigenfrequencies for which this occurs can be calculated [4, p. 53] from

f = ( c / 2 ) [ ( l / L )² + ( w / W )² + ( h / H )² ]^1/2 [Hz] (1)

If the largest room dimension is the length L and l = 1, w = h = 0, then the lowest frequency is

f_min = c / 2 L [Hz] (2)

In the above example room with L = 7.63 m (25 ft) and c = 344 m/s, the lowest frequency is f_min = 22.6 Hz. Below this frequency the sound pressure is no longer a function of location in the room. Its absolute level is determined by the absorption characteristics of the six boundary surfaces and the materials in the room.

At 22.5 Hz, the 7.63 m (25 ft) room length corresponds to a half wavelength of sound. The sound particle velocity is zero at all times on the surfaces of the front and rear walls. The sound pressure on each surface varies at the 22.5 Hz rate as the sound wave travels back and forth between them. This is a resonance condition that can be described by a second order system with a resonance curve of width BW [Hz] at the half power or -3 dB points. When the excitation is removed, the sound pressure will decay by 60 dB in a time

T₆₀ = 2.2 / BW [s] (3)

If the excitation is applied as a step function, then the sound pressure will rise from 10% to 90% of the steady-state level during a time

T_rise = 0.7 / BW = 0.32 T₆₀ [s] (4)

Equations (1) through (4) will be useful in interpreting measured room transfer functions later on. The eigenfrequencies from equation (1) are readily tabulated in a spread sheet (Fig. 1) for various permutations of l, w and h. 

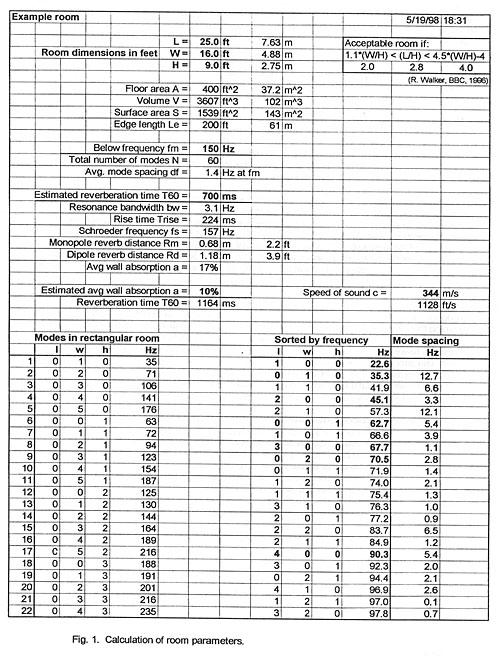
The spacing of eigenfrequencies is initially irregular and wide but decreases rapidly as frequency increases. The number of eigenfrequencies between zero and a given upper frequency limit f_m can be estimated [4, p.56] from

where

V = L W H [m³]

S = 2 ( L W + L H + W H ) [m²]

L_e = 4 ( L + W + H ) [m]

and assuming n = 2.5 eigenfrequencies per bandwidth, we can calculate a lower frequency limit, f_s , above which the separation of modes is so small that the room is more appropriately analyzed on a statistical basis rather than by discrete modes of resonance [4, p. 67].

f_s = 1900 ( T₆₀ / V )^1/2 [Hz] (8)

For the example room this frequency is 157 Hz and is approximately the low end of the reverberant mode region for the sound pressure distribution in the room. It is also the upper frequency limit for this investigation into sound quality differences between monopolar and bipolar low frequency radiators.

When we consider radiation in the reverberant frequency range, the sound at the listening position is composed of the direct sound from the source and the reverberant sound that is more or less uniformly distributed in the room. The direct sound pressure level decreases inversely to distance from the source and will equal the reverberant sound pressure at distance R_G. The ‘reverberation distance’ [4, p.118] is calculated from

where the directionality gain G is unity for a monopole and G = 3 for a dipole [5]. A dipole, thus, has a 3^1/2 = 1.73 times larger reverberation distance. Correspondingly, for a dipole the ratio of direct to reverberant sound pressure level is 4.8 dB greater than for a monopole. A typical reverberation distance is quite small, 0.68 m for the monopole and 1.18 m for the dipole in the example room. Thus, at 3 m distance from the source, the direct sound would be 12.9 dB below the reverberant sound field for the monopole and 8.1 dB for the dipole. The 4.8 dB lower level of the reverberant field in the case of the dipole is significant by subjectively reducing the masking influence of the room upon sonic detail, by avoiding the sensation of overload of the room during loud passages of program material and by being much less noisy to neighbors. Even at reduced level the spectral balance of the reverberant field is important for naturalness of sound reproduction [3].

Several investigators have studied the distribution of eigenfrequencies in order to arrive at optimum room dimensions. In the range below f_s the separation between eigenfrequencies may vary considerably. Fig. 2 shows this for the example room. 

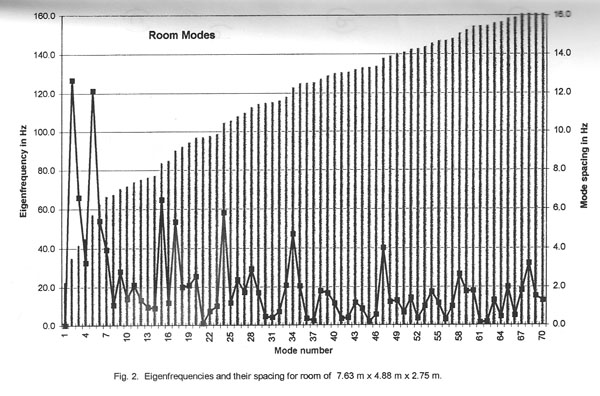
Bonello [6] counts the number D of eigenfrequencies in each one-third octave band between 10 Hz and 200 Hz and proposes criteria for the allowed variation of D with frequency. Walker [7] squares the frequency difference between each pair of eigenfrequencies, takes their sum and divides it by the number of eigenfrequencies included. This procedure gives greater weight to undesired widely spaced pairs in the resulting room quality index. The index was calculated for rooms of different sizes and proportions. A room is deemed acceptable if it meets the inequalities

1.1 ( W / H) < ( L / H) < 4.5 ( W / H ) - 4 (10)

The example room meets this criterion with 2.0 < 2.8 < 4.0.

In these investigations, though, no consideration is given to source type, source position and listener position in the room. Modes at all eigenfrequencies are assumed to be of equal strength. Yet, a monopolar pressure transducer will primarily excite those modes for which it is located near a pressure maximum. Only if placed in a room corner will it excite the maximum number of modes. A dipolar radiator, which is a velocity transducer, will excite modes when placed near their particle velocity maximum. In a rectangular room, though, there exists no location which is a velocity maximum for all modes, equivalent to the pressure maximum in a room corner. A dipole, being directional, will always excite fewer than the total number of possible modes.

The purpose for reviewing the modal behavior of the room is to gain insight into how a room of given size and proportions will affect the sound transmission from woofer to listener [8, 9]. It is assumed that the steady-state room transfer function contains information that explains the differences between monopolar and dipolar radiation.

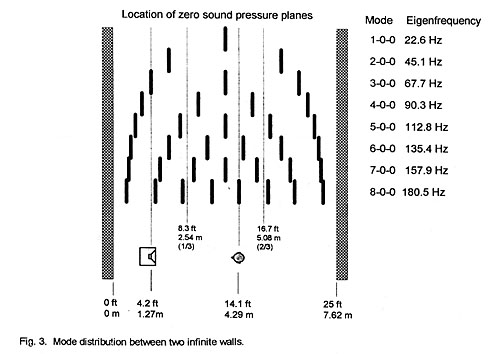
A greatly simplified model will be used for the room. By restricting the analysis to the length dependent eigenfrequencies we only deal with reflections from the front and rear wall. In equation (1) the coefficients w and h are zero. For the 7.63 m (25 ft) long example room all eigenfrequencies are then multiples of 22.6 Hz. The woofer is placed at 1.27 m (4.2 ft) from the front wall and the listener at 4.29 m (14.1 ft). These locations are chosen as somewhat typical for a loudspeaker setup and place the woofer in the pressure null of the 3-0-0 mode and the listener in the null of the 8-0-0 mode (Fig. 3). 

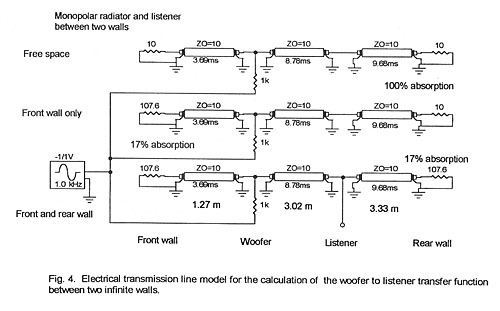
The analysis is carried out using a lossless transmission line model to describe the acoustic path (Fig. 4). An assumed wall absorption coefficient of 17% is realized by terminating the lines with a 83% reflecting load.

Two steady-state transfer functions are shown in each of the following figures. The first is the response with the wall behind the listener removed to indicate the effect of the front wall reflection. The second response includes both front and rear wall. Comparing the two curves points out the marginal usefulness of an analysis that only considers the wall behind the speaker. The same can be concluded about a speaker placement analysis for two intersecting walls only or for a corner [10] that ignores the other walls. The opposite wall always produces a strong influence on the overall response unless it is highly absorptive, which is very difficult to achieve at low frequencies.

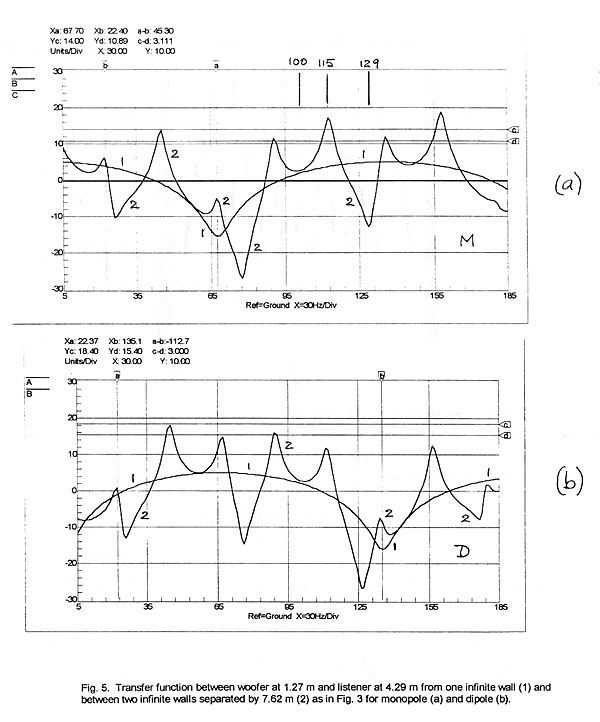
The steady-state transfer functions in Fig. 5a are for the monopole, those in Fig. 5b for the dipole. The responses are quite different for the two types of radiators, although it is difficult to conclude that either is superior. The dip due to the front wall reflection occurs for the dipole at twice the frequency of the monopole’s dip. The monopole is situated at the pressure minimum of the 67.7 Hz 3-0-0 mode (Fig. 3) and the response has, indeed, a depression at this frequency but it also coincides with the dip from the front wall reflection. The dipole has a peak at 67.7 Hz by being at the velocity maximum, but this peak is still lower in amplitude than the one at 45.1 Hz for the 2-0-0 mode, even though the dipole is not at a velocity maximum location for that mode. The preceding shows that peaks in the response curve match the eigenfrequencies, but their relative amplitudes are not easy to predict. The -3 dB bandwidth of the resonances is constant at 3 Hz, corresponding to a 700 ms decay time for 17% absorption (Equ. 3, 7).

The same analysis is carried out with the room length divided into thirds (Fig. 6). This type of setup is frequently talked about in audiophile circles. It is not apparent why the resulting response should be an improvement over the one in Fig. 5, nor that it has particular benefits for monopolar radiators for which it is recommended.

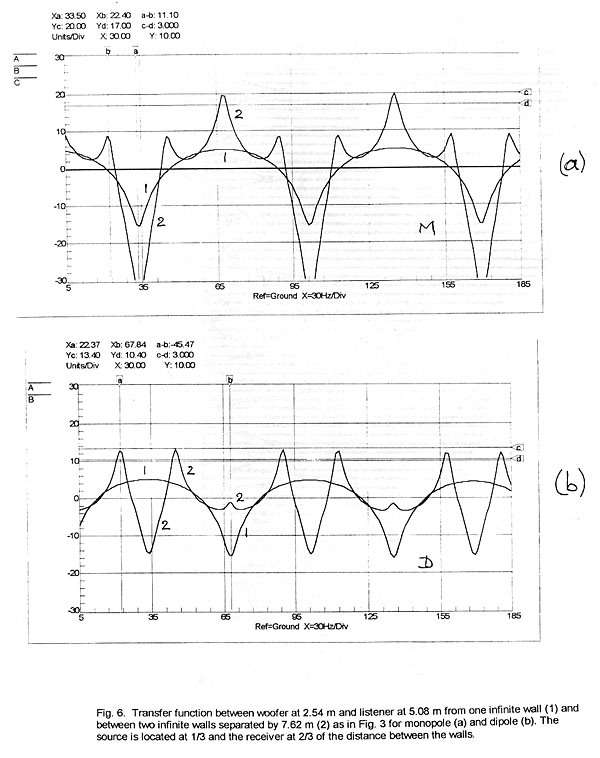
When we look at the response in the time domain by applying a 113 Hz signal to excite the 5-0-0 mode (Fig. 5), we see that it takes 224 ms (Fig. 7) to reach 90% of steady-state, as was calculated from Equ. 4. At 129 Hz where the steady-state frequency response dips we observe an oscillatory behavior of a low amplitude time waveform, and at 100 Hz, between two resonance peaks, the response builds up quickly but with overshoot and ringing.

As simple and incomplete as this model is for the analysis of the room transfer function, it still points out the complexity of the response in both time and frequency domains. It does not seem possible, though, to draw conclusions about qualitative differences between omnidirectional and directional woofers using this method alone since the model examines propagation only along one axis. Different techniques will have to be used to obtain a more complete picture.

A loudspeaker in a room can be modeled with image sources to describe the multiple reflections from the six boundary surfaces. This method allows us to take directivity into account as well as wall absorption. Both steady-state and impulse response can be calculated but the method is computationally intensive.

Ray tracing techniques which are often used to investigate large spaces are not appropriate for this case because they are based on the assumption that the wavelengths of sound considered are vanishingly small compared to the room dimensions and wall surfaces.

Finite element methods, FEM, can give a solution for the steady-state sound pressure at any location in the room, but only one frequency at a time. Time domain based step wise solutions to the propagation of sound from the speaker provide a complete description of the sound field in time and frequency, but require large amounts of computation.

All techniques are limited when trying to model real rooms with irregular shapes, windows, openings and furniture of varying absorption and diffusion properties. Yet, this is the usual environment for listening to stereo and home theater.

A special woofer was constructed to allow immediate selection of either omnidirectional or dipolar radiation without having to move any equipment. The woofer contains two 300 mm (12 inch) drivers at each end of a 0.36 m x 0.36 m x 0.53 m (14 in x 14 in x 21 in) rectangular box. The two drivers operate in-phase for monopolar and out-of-phase for dipolar radiation. The free field response is equalized in each configuration to be flat over the frequency range of interest.

The steady-state response at the listening position for a radiator in a room may be measured with a sine wave sweep or calculated from the measured impulse response. The frequency sweep must be sufficiently slow for the room response to reach steady-state behavior. Each resonance in the response must be traversed much slower than the rise time for that resonance. With a sweep rate SR in Hz/s and Equ. (4) we can write

BW / SR > 0.7 / BW

SR < 1.4 BW² [Hz/s] (11)

For BW = 3.1 Hz the sweep rate must be less than 13.5 Hz/s. It would require over 7.4 s to sweep a 100 Hz frequency range so that the response can reach its steady-state at each resonance.

The same room response data may be gathered from a 1 s long record of the impulse response which provides us with a 1 Hz data point resolution after the impulse response has been Fourier transformed into the frequency domain. A maximum length sequence signal analyzer is used to acquire the long impulse response.

Initial measurements were performed in a small office room. This room has length-width-height dimensions of 3.45 m x 3.05 m x 2.75 m (11.3 ft x 10 ft x 9 ft). It is fully enclosed, furnished with desks, book shelves, cabinets, pictures on the walls and has a hardwood floor. Ten percent of the room’s surface area is double pane window glass. The woofer was placed on the floor, approximately in the center of the room, and the microphone near an upper room corner.

The steady-state room transfer function for this particular setup was measured for monopolar and dipolar radiation. The two responses in Fig. 8 are quite different from each other and neither is particularly appealing. The narrowest peaks have a -3 dB width between 3 Hz and 4 Hz indicating an approximate decay time of T₆₀ = 600 ms at these resonances (Equ. 3). The calculated eigenfrequencies are drawn as short vertical lines in these figures. The axial modes are separated out, because they are often considered to dominate the room response. From Equ. 5 a total of 41 modes are estimated to be possible below 200 Hz. Of interest is the correlation between the variations in the transfer function curve and the known eigenfrequencies.

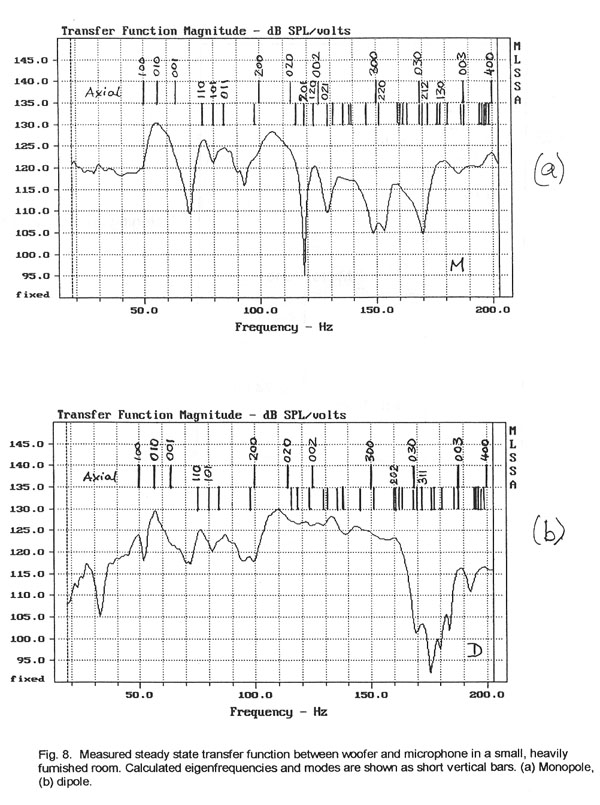
It can be seen immediately that below the 1-0-0 mode with f_min = 50 Hz the monopole response stays constant while the dipole response rolls off. A dipolar radiator progressively looses its ability to pressurize a closed room as frequency decreases below f_min . A comparison of the peaks and dips in the two response curves to the eigenfrequency lines above them shows that for this room there exists a correlation between some lines and the curve and none for other lines. The nature of correlation, i.e. peaks or dips at the same eigenfrequency, is occasionally the same yet often different for the two types of radiators. The axial room modes do not dominate the curve features but correlate more with peaks than dips for their lower orders. Tangential and oblique mode frequencies also correlate, and more so for the monopole than for the dipole radiator.

We must conclude from this and other similar measurements that it is nearly impossible to predict any detail in the measured frequency response from a prior knowledge of the room’s eigenfrequencies and their spectral distribution. Eigenfrequency calculations are useful, though, in trying to understand how details in the measured response curve might relate to the given room dimensions and the placement of woofer and listener.

The two responses in Fig. 8 say little about potential quality differences between dipolar and monopolar woofers other than that a larger number of modes can be correlated to the monopolar response curve and that the dipolar curve appears smoother.

The following acoustic measurements were performed in a much larger room, Fig. 9. Its acoustic length is difficult to define because the basic rectangle of 4.88 m (16 ft) width and 17.37 m (57 ft) length is interrupted by openings to a hall and a staircase and by partial walls at 10.36 m (34 ft) of its length. The height of the room is 2.74 m (9 ft) but a section above the listening place is raised to 4.57 m (15 ft) in form of a clarestory. The sides have large floor to ceiling window areas. The hardwood floor is partially covered with carpets and rugs. The room is furnished as a normal living room without further acoustic treatment. The test woofer is placed in about the location of the left channel woofer of the normal stereo sound system and the microphone at the listening position.

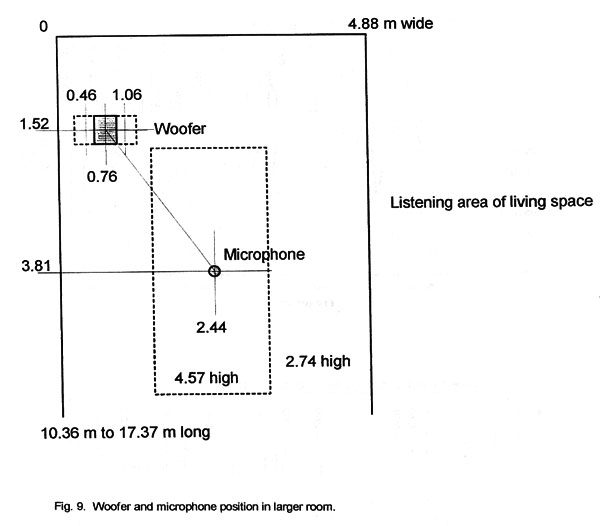
The steady-state transfer function is measured first for the monopolar radiator as it is rotated in 15 degree increments towards the microphone and as it is shifted laterally +/-0.30 m (1ft) from its reference position (Fig. 10). Below 130 Hz the test woofer behaves, indeed, like a monopole but it becomes increasingly directional at higher frequencies because of the 0.53 m (21 in) length of the box between the drivers. The transfer function is more sensitive to lateral shifts. The woofer output increases over a wider frequency range with increasing proximity to the side wall (Fig. 10b) than for rotation.

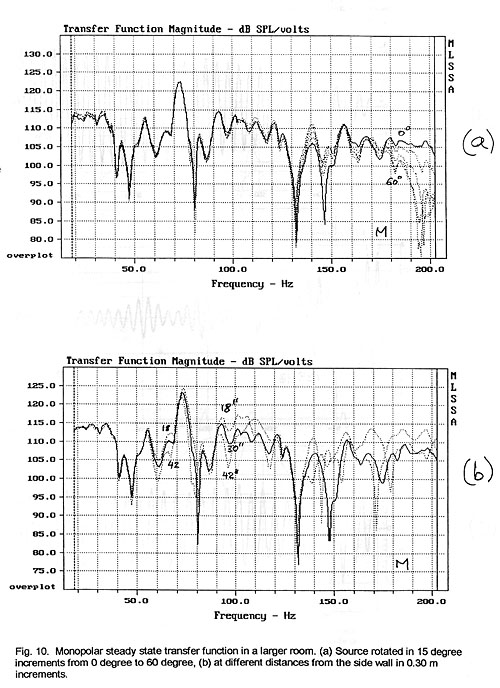
The same measurements for the dipolar radiator indicate similar sensitivity to lateral shifts but considerably different behavior versus rotation (Fig. 11). Under free field conditions a rotation of sixty degrees from the main axis would reduce the output to cos 60⁰ = 0.5 or to -6 dB. The observed variation in the room depends upon frequency but becomes more uniform above 150 Hz. Taking this and the monopolar behavior above 130 Hz into consideration we conclude that in the frequency range above approximately 150 Hz, where mode density becomes high, the response is dominated by the directivity of the source and not by room modes.

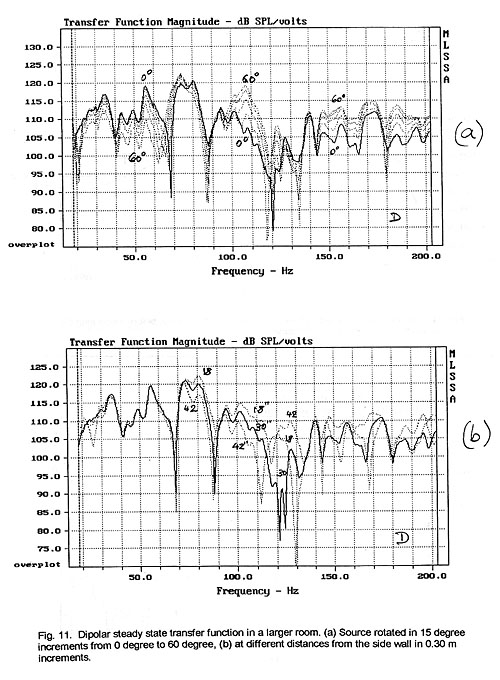
The dipolar and monopolar radiation transfer functions are quite different from each other yet it is not obvious how to derive performance differences from these two, purely frequency domain, steady-state response data sets.

A display of the associated cumulative spectral decay plots, though, provides some insight into the nature of the more dominant features of the steady-state response (Fig. 12 to Fig. 13). The strong resonance at 73 Hz decays smoothly for the monopole (Fig. 12) but is broken up and widened for the dipole (Fig. 13). The dipole’s range above 100 Hz is more random in its decay from one spectrum slice to the next one 5 ms later. Viewed from the reverse perspective (Fig. 12b, 13b), it is of interest how the deep notches in the steady-state response are filled by the reverberant spectrum after about 20 ms of decay. It points out that the perceptual effect of these cancellations, visible primarily in the steady-state response, is likely to be masked and no attempt should be made to equalize them with narrowband high gain electronic filters [11]. Equalization would add excess narrowband sound energy to the decay.

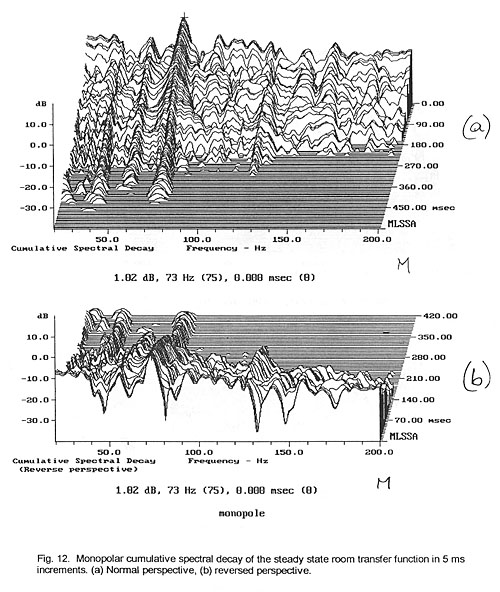
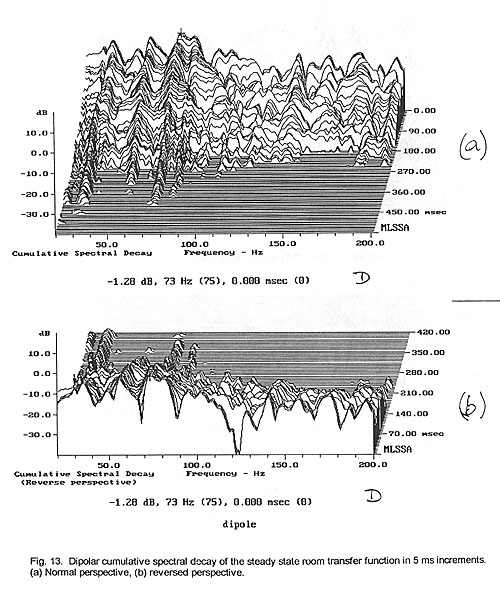
Convincing qualitative differences are difficult to derive from a visual inspection of these decay plots, although some measure of time domain behavior is displayed. Note that only the decay of sound with time has been shown and the initial build up of sound pressure has been ignored [12]. This missing information is contained in the impulse response. A display of the impulse responses for monopolar and dipolar radiation, though, does not readily reveal clearly discriminating features.

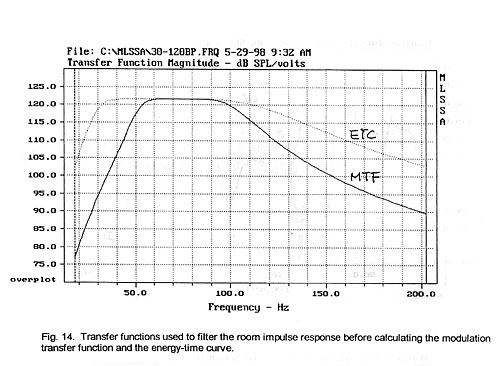
To investigate the impulse response further its spectral content is restricted to the 30 Hz to 120 Hz range of interest by bandpass filtering (Fig. 14). Then the Energy-Time Curve (ETC), i.e. the envelope of the magnitude of the filtered impulse response, is calculated (Fig. 15). We see that the energy of the dipole is lower after the initial response peak than that of the monopole. Theoretically, the sound pressure of the reverberant field should be 4.8 dB lower for an ideal dipolar radiator [5]. The initial 40 ms of sound energy, in this example, are more separated from the remainder of the decay than for the monopole. The monopole shows little variation over the first 120 ms before it falls off more or less monotonically. This behavior might be influenced by the strong 73 Hz resonance seen in Fig. 12. The temporal behavior of the dipole’s decay in Fig. 13 is not clearly visible, but it appears to follow the periodicity of decay in the ETC curve.

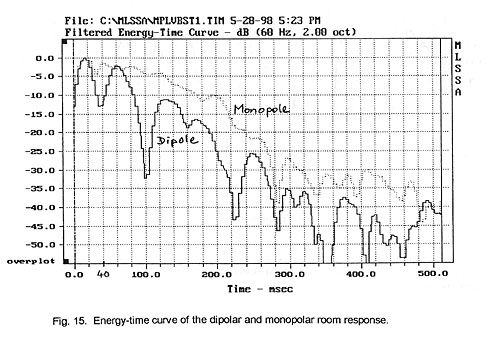
The widely reported subjective perception of greater articulation from dipolar bass reproduction could be attributed to the lower energy after the initial signal onset and to the gaps in reverberant energy flow. The gaps might be caused by a less uniform spatial excitation of modes from a directional source. These preliminary observations should be investigated further.

The modulation transfer function, MTF, is typically used to analyze speech intelligibility in reverberant spaces [13]. In principle, an octave wide band of noise in the speech frequency range is amplitude modulated at different modulation frequencies. The signal is radiated into the room under investigation and monitored at different locations in the room. The reverberant field, i.e. signals arriving from multiple directions at the receiver, tend to fill in the valleys in the modulation envelope of the octave noise. The reduction in modulation depth from the original 100% is measured versus modulation frequency and is an indicator of articulation loss. Alternatively, the desired information can be derived from the system impulse response [14 15]. The MTF describes the time domain behavior of a system versus center frequency of the noise band and versus modulation rate. The modulation frequency sidebands in the transmitted spectrum are symmetrically offset above and below the center frequency. As the modulation frequency varies the coherence between symmetrical spectral areas is tested.

The MTF is an indicator of how well amplitude fluctuations of a signal are preserved under the masking influence of room resonances, reverberation and reflections. In the low frequency range the MTF should predict the preservation of vibrato and bass instrument sonic detail.

A center frequency of 73 Hz and a one octave noise bandwidth (Fig. 14) were chosen to measure the MTF of the living room setup over a 52 Hz to 103 Hz frequency range for the monopolar and dipolar woofer configuration (Fig. 16). In this frequency range the previously shown room resonances should have their strongest effect. The two transfer functions are different and favor the dipole at most modulation frequencies. Only between 9.5 Hz and 13 Hz is the monopole superior, but the depth of modulation for either is very low.

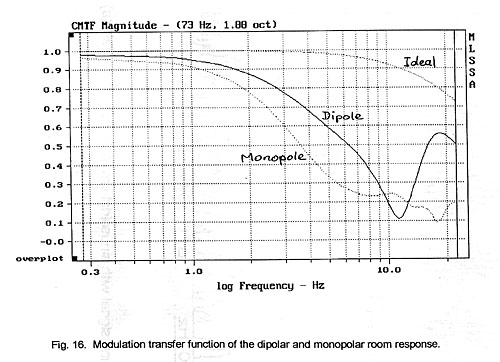
Also shown is the response of an ideal system. Its modulation depth decreases with increasing modulation frequency because the sidebands of the amplitude modulation spectrum are attenuated by the corners of the bandpass filter response. The dipole and monopole curves must be compared to the ideal response to see the actual degradation of the modulation depth due to room modes.

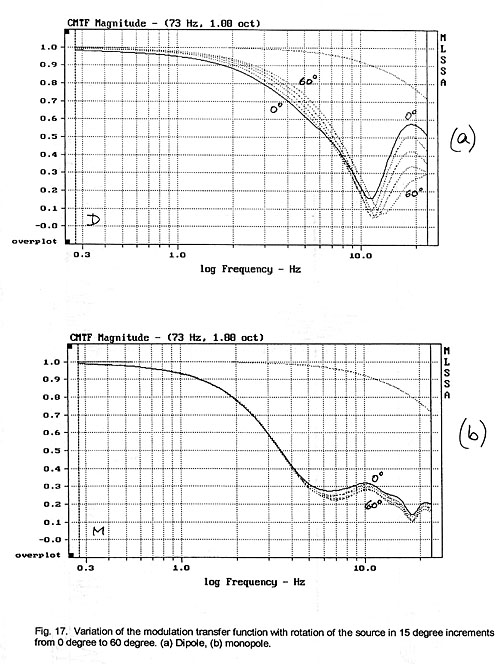
As expected the MTF is sensitive to angular rotation of the dipole source (Fig. 17a), unlike the monopole source which is mostly insensitive to changes in angular position (Fig. 17b). The MTF improves for the dipole in this particular room setup for modulation rates below 10 Hz but degrades for higher rates as the woofer is turned towards the microphone.

A shaped tone burst signal consists of a few cycles of a sinewave with an amplitude envelope from one of the standard FFT window functions. The envelope shape and its duration determine the width and shape of its spectrum coverage [16]. For example, a ten cycle burst with a sinusoidal envelope has a spectrum coverage of about one-third of an octave centered at the burst frequency (Fig. 18a). The response of a system to this type of test signal is observed on an oscilloscope. A shorter burst of fewer than ten cycles would provide faster rise and decay times and reveal finer temporal detail about the system under test, but would sacrifice frequency resolution by exciting more than a one-third octave frequency range. In general, a tone burst test will show neither the detail in amplitude response variation of the swept sine wave test nor the rapid amplitude fluctuations of a wide band pulse test [17]. The sine wave stimulates the system one frequency at a time while an impulse excites the system with all frequencies simultaneously. The shaped tone burst falls somewhere in between these two cases. Depending on the burst shape, the test signal emphasizes either the steady-state or the transient characteristics of a system. A further benefit of this method stems from the fact that our hearing responds to both temporal and timbrel cues and the shaped tone burst is thought to elicit a system response that is closer to the way we perceive sound.

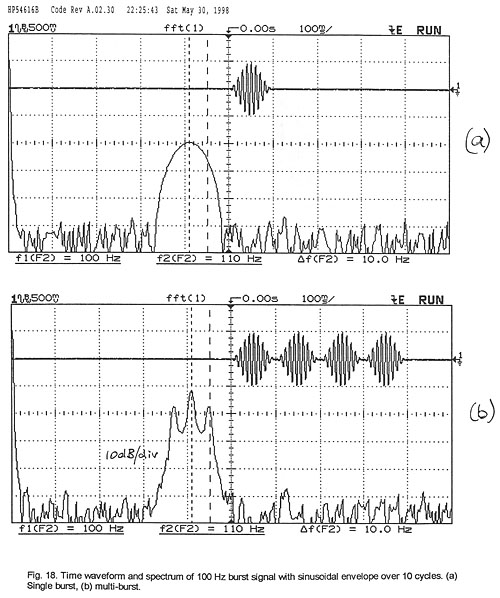
When multiple shaped tone bursts are strung together, then the resulting signal has the characteristics of a short section of a 100% amplitude modulated waveform (Fig. 18b). The modulation rate f_M for a burst of n cycles of frequency f_B is

f_M = f_B / n [Hz] (12)

Four bursts of 10 cycles each of a 100 Hz sine wave would thus represent a 40 cycle section of a 100 Hz carrier which is 100% amplitude modulated at 10 Hz rate.

The multi-burst waveform has some similarity to the test signal used for the MTF measurement [12]. The difference being that the octave band of noise has been replaced by a continuous sine wave as carrier of the modulation and the modulation rate has become a fixed percentage of the carrier frequency.

With four bursts of a 100 Hz carrier the duration of the test signal becomes 400 ms. This is longer than the 230 ms rise time (Equ. 4) of a typical 3 Hz wide peak in the steady-state frequency response. The system response to the multi-burst signal will, therefore, reach its steady-state. The forty cycle test signal seems well suited for room measurements below 200 Hz. The signal is generated with an arbitrary waveform generator (HP 33120A) and observed on an oscilloscope with digital storage (HP 54616B). Other test signals were tried, such as a 5 Hz amplitude modulated continuous carrier or two bursts for the multi-burst signal. The four burst signal was found to be superior in providing timbrel and temporal information about the room response.

When the received signal is observed on an oscilloscope and listened to at the microphone location or through the microphone, changes in waveform appearance on the oscilloscope can be related to subjectively perceived variations in sound character. Similar to the MTF, on the oscilloscope we expect to see a degradation of the modulation envelope due to room resonances.

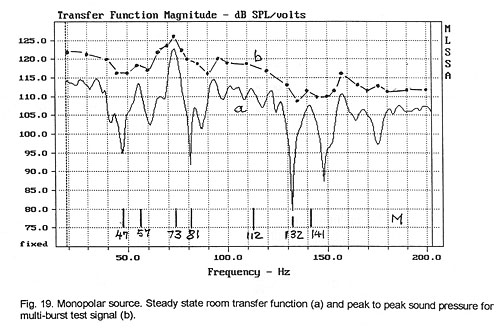
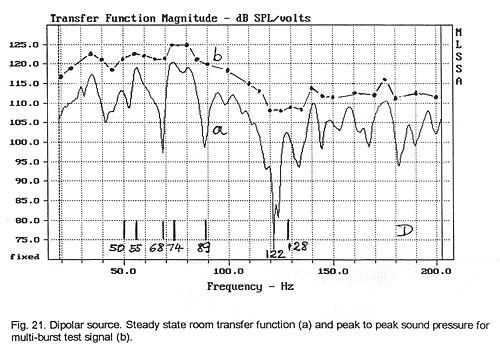
The multi-burst transfer function was measured using the same setup of woofer and microphone as was used for the steady-state frequency response measurements above. When the monopolar and dipolar responses are compared to the steady-state responses (Fig. 19 and Fig. 21), then the smoothing effect of the test signal upon the transfer function is readily seen. The peak-to-peak amplitude of the burst as read from the oscilloscope was converted to dB and plotted. The same measurement could be carried out with a peak reading sound level meter (e.g. RS 33-2055). The amplitude variation of the burst response from frequency to frequency corresponds much more closely to what is heard with program material than the variation seen in the steady-state response. These variations are also easily audible.

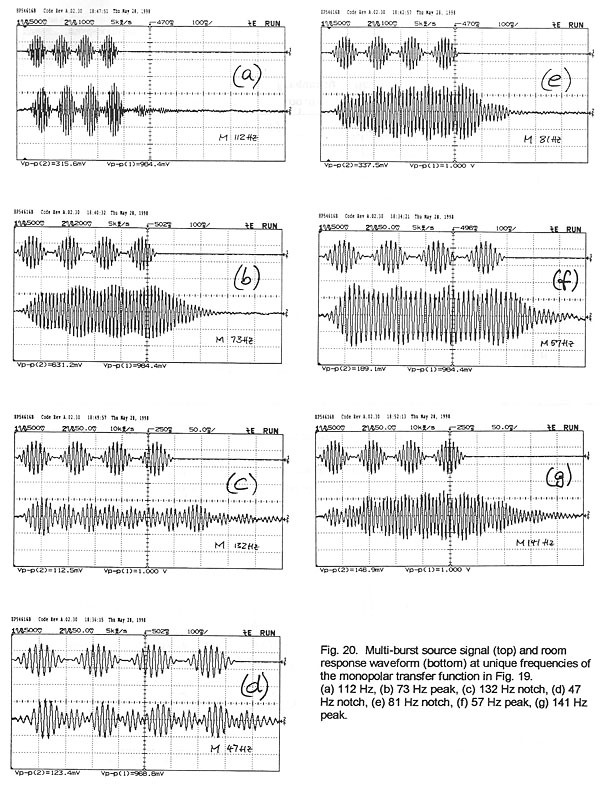
Of particular interest is the relationship between the different details of the steady-state frequency response when compared with the waveform of the multi-burst signal. For example, at 112 Hz of Fig. 19 there is a slight degradation of the waveform (Fig. 20a), but the signal is well articulated when listened to at the microphone location, which means that the 11.2 Hz modulation is audibly well preserved. At 73 Hz, though, the modulation has almost disappeared (Fig. 20b). The sound drones on and is quite loud. Investigating the cancellation notch at 132 Hz we find not only a loss in articulation (Fig. 20c) but also a change in sound character and timbre. The modulation envelope appears to have twice the original rate. The effect is caused by the interference of two modes with opposing phase shifts. In some cases this is audible as out-of-phase sound arriving from two different directions. Similar effects can be observed at 47 Hz (Fig. 20d) and 81 Hz (Fig. 20e). The peak in the steady-state response at 57 Hz produces a loss in articulation of the burst (Fig. 20f), but the peak at 141 Hz (Fig. 20g) causes less of a perceived loss even though the waveform would suggest otherwise.

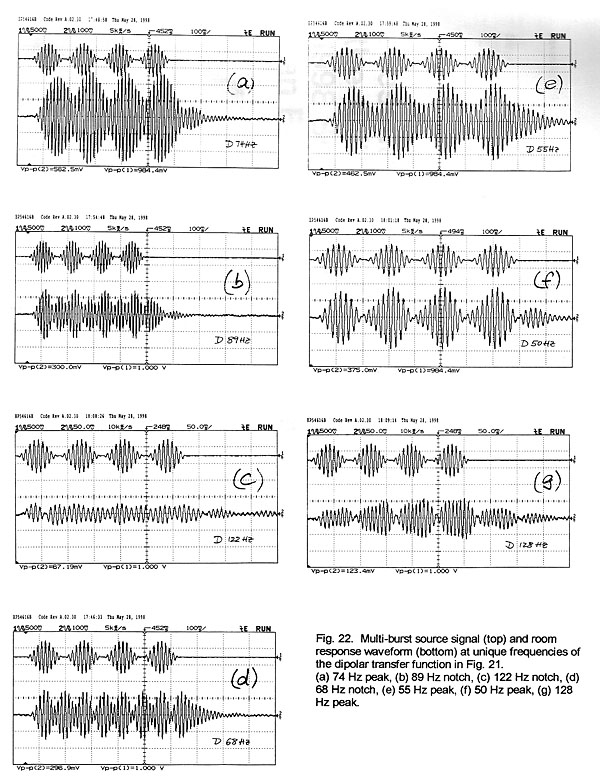
When we examine the dipolar burst response (Fig. 21) at the 74 Hz peak in the steady-state frequency response, we find that the signal is audibly louder at this peak but the articulation is not smeared (Fig. 22a). The dip at 89 Hz still maintains articulation, again, not in full agreement with the observed waveform (Fig. 22b). The dip at 122 Hz, though, is associated with a significant audible deterioration of the signal (Fig. 22c), as is the notch at 68 Hz (Fig. 22d). The behavior at peaks in the frequency response is also not always consistent. The peak at 55 Hz is perceived as degrading the modulation (Fig. 22e), while the peaks at 50 Hz and 128 Hz maintain good articulation (Fig. 22f and Fig. 22g).

It is difficult to show pictorially and quantitatively the perceived differences when listening to the reproduced multi-burst test signal from a monopolar and a dipolar low frequency radiator in a room. After examining the two steady-state frequency responses with the multi-burst signal over the whole frequency range under investigation and in small 1 Hz frequency increments, it was concluded that the dipolar radiator has fewer and less pronounced regions of loss in articulation, on average, than the monopolar radiator. The strong 73 Hz resonance excited by the monopole is a major factor in its subjectively degraded performance. This might be correctable by electronic equalization but the dipole would require less of such remedy since it inherently couples to fewer room modes.

This investigation into sound quality differences between monopolar and dipolar woofers in small rooms has shown the difficulty of relating visual displays of various forms of data to perceived sound differences. It has also shown the difficulty of finding those parameters that should be measured in order to explain what is heard. This work should be considered as preliminary and encourage other investigators to search further. Several conclusions can be drawn, though, from the investigation into low frequency sound reproduction from directional and non-directional woofers in small rooms.

A valuable outcome of the investigation is the development of the multi-burst test signal. Its frequency should be adjustable in < 2 Hz increments between 20 Hz and 120 Hz and in < 5 Hz steps up to 200 Hz. The time intervall between bursts is preferably > 1.5 s to give the auditory system time to reset.

The test signal is well suited for objective and subjective evaluation of low frequency room acoustics. At any given test frequency we can hear not only the sound pressure variation versus location in the room as we walk around, but more importantly we can hear changes in sound quality in the form of articulation versus "boom" or "muddiness". The test signal allows one to hear the effect of changing woofer placement or listening position upon articulation and uniformity of frequency response. It can be used to evaluate the subjective effect of low frequency room equalization or to determine the placement and effectiveness of sound absorbers.

The investigation showed that measurable and audible quality differences exist between monopolar and dipolar woofers due to differences in their respective interactions with the room. The degree of these differences is difficult to predict and will depend upon the specifics of a room and the placement of woofer and listener. However, the dipolar source can be expected to interact less strongly with the room and will, therefore, on average convey greater detail and resolution of complex low frequency material.

[1] J. Salmi, Dipole Source Placement in a Room, 92nd AES Convention, 1992 Vienna, Preprint 3327

[2] C. Ferekidis and U. Kempe, Room Mode Excitation of Dipolar and Monopolar Low Frequency Sources, 100th AES Convention, 1996 Copenhagen, Preprint 4193

[3] S. Linkwitz, Development of a Compact Dipole Loudspeaker, 93rd AES Convention, 1992 San Francisco, Preprint 3431

[4] H. Kuttruff, Room Acoustics, John Wiley & Sons, 1973, ISBN 0-470-51105-2

[5] L. L. Beranek, Acoustics, McGraw-Hill, New York, 1954, Chapter 4

[6] O. J. Bonello, A New Criterion for the Distribution of Normal Room Modes, J. Audio Eng. Soc., Vol. 29, No. 9, 1981 September, pp. 597-606

[7] R. Walker, Optimum Dimension Ratios for Small Rooms, 100th AES Convention, 1996 Copenhagen, Preprint 4191

[8] T. Salava, Acoustic Load and Transfer Functions in Rooms at Low Frequencies, J. Audio Eng. Soc., Vol. 36, No. 10, 1988 October, pp. 763-775

[9] T. Salava, Low-Frequency Performance of Listening Rooms for Steady-State and Transient Signals, J. Audio Eng. Soc., Vol. 39, No. 11, 1991 November, pp. 853-863

[10] K. O. Ballagh, Optimum Loudspeaker Placement Near Reflecting Planes, J. Audio Eng. Soc., Vol. 31 No. 12, 1983 December, pp. 931-935

[11] P. Craven, M. Gerzon, Compensating Filters, US Patent 5,511,129, April 23, 1996, Background of the Invention

[12] G. Adams, Time Dependence of Loudspeaker Power Output in Small Rooms, J. Audio Eng. Soc., Vol. 37, No. 4, 1989 April, pp. 203-209

[13] T. Houtgast, H.J.M. Steeneken, The Modulation Transfer Function in Room Acoustics as a Predictor of Speech Intelligibility, Acustica, Vol. 28, 1973, pp. 66-73

[14] M. R. Schroeder, Modulation Transfer Functions: Definition and Measurement, Acustica, Vol. 49, 1981, pp. 179-182

[15] D. D. Rife, Modulation Transfer Function Measurement with Maximum-Length Sequences, J. Audio Eng. Soc., Vol. 40, No. 10, 1992 October, pp. 779-790

[16] S. Linkwitz, Shaped Tone-Burst Testing, J. Audio Eng. Soc., Vol. 28, No. 4, 1980 April, pp. 250-258

[17] O. Dossing, Uncertainty in Time/Frequency Domain Representations, Sound and Vibration, Vol. 32, No. 1, January 1998, pp. 14-24

[18] Observation based on transfer function measurements in a solid walled room of 8.74 m x 5.69 m x 3.15 m (L x W x H) with predominantly length modes at multiples of 19.7 Hz, at residence of S. Dickson, Honolulu, Hawaii, May 1998

----------------------------------------------------------------------

See also: