|
Digital Photo Processes-- Introduction -- Lens & image -- A/D conversion -- Lumix & Leica -- Sharpness -- CCD noise1 -- CCD noise2 -- 5 years later --
Focal length, physical size, aperture and
depth-of-field
|
 |
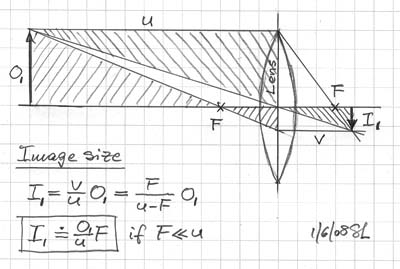 |
The image size I1 produced by a lens for a given object O1 at distance u in front of it, is directly proportional to its focal length F.
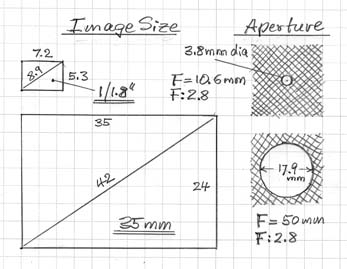
Thus, if some object filled the frame of a 35mm film camera through a 50mm lens, then that object would also fill the frame of a 1/1.8" sensor on a digital camera, like the FZ50, when its focal length is zoomed to 50mm / 4.73 = 10.6mm. Both cameras have the same angle of view in this instance.
If both lenses have the same aperture F:2.8, then in one case the diameter of the opening is 50/2.8 = 17.9mm and 10.6/2.8 = 3.8mm in the other. Obviously the larger diameter opening lets 4.732 = 22.4 times more photons pass through in a given amount of time. Therefore the larger format camera could be almost 4.5-stops (24.5 = 22.6) more sensitive to light than the small sensor camera, everything else being equal. At ISO 1600 it could have the same signal to noise ratio as the small one at ISO 100.
The small sensor size allows for a small physical size of the lens and the camera body, but sacrifices low light performance. Furthermore, the precision of the lens manufacturing process has to be higher if the same resolution in lines/mm is to be obtained as for the larger format lens. If the final output is an 8" x 10" print which has a 325mm diagonal, then the large format frame is magnified only by 325/42 = 7.7 times, but the small format by 325/8.9 = 36.5 times or 4.73 times more.
The small physical size of the aperture opening leads to decreased resolution at the highest F-stop settings due to diffraction of light rays at the edge of the opening. For example, the aperture diameter for the 10.6mm lens at F:11 is only 1mm or 1000 mm. The wavelength of visible light is in the range of 0.4 to 0.8 mm and no longer negligible in comparison. These small lenses are probably optimally used wide open.
So is there any benefit from a small sensor besides its lower manufacturing cost and its leading to smaller camera sizes? Possibly the depth-of-field. It is larger for the short focal length lenses which makes focusing less critical. Numerically the 10.6mm lens on the FZ50 at F:2.8 has 4.73 times more depth-of-field than the 50mm lens at F:2.8. It would be equivalent to 4.73 x F:2.8 = F:13.2 in the larger format. This can be of advantage in landscape photography but is usually of great disadvantage in portrait photography.
Compact digital cameras give no indication on the lens body of the depth-of-field range for different apertures and focusing distances. It would be important to know for short focusing distances and in macro photography which these cameras are readily capable of. The Lumix LX2 indicates depth-of-field by a bar graph on its LCD monitor when switching the lens to manual focus mode even when it has focused automatically.
The above discussion shows trends and limitations that make me appreciate what has been accomplished in compact camera design. It would be nice if the maximum lens aperture could be increased to F:2.0 on a future LX2 without reducing the sensor size. The older Olympus C-5050 which I own has a F:1.8 lens and 5 Mpixel resolution with its 1/1.8" sensor. Unfortunately it is bulkier than what I would like to carry with me.
|
FZ50 |
max Wide (35mm equiv.) | max Tele (420mm equiv.) | Ratio |
| Focal length, F | 7.4 mm | 88.8 mm | 1 : 12 |
| Aperture, A | F:2.8 | F:3.7 | 1 : 1.32 |
| Aperture diameter, F/A | 2.64 mm | 24.0 mm | 1 : 9.1 |
| Image diagonal, I2 (1/1.8") | 8.9 mm | 8.9 mm | 1 : 1 |
| Angle of view, I2/F 1) | 690 | 5.70 | 12 : 1 |
| Exposure time, T, e.g. | 1/80 sec | 1/60 sec | 1 : 1.33 |
It is interesting to note that the aperture diameter of a lens increases with its focal length F. You can also see this as you look into the lens. The opening becomes larger and thus it would seem that more photons are captured in a fixed amount of time. But since the angle of view narrows with increasing focal length, proportionally fewer photons are seen by the lens. Thus the increase in diameter is compensated by the decrease in angle of view. The same number of photons is captured in the given amount of time regardless of focal length F as long as the aperture A remains constant. In the above table it can be seen that the exposure time T changes in proportion to the aperture A when measuring the light reflected from a neutral gray surface.
T = const x (A / F) x (F / I2) = const x A / I2
A 420mm telephoto lens with F:3.7 opening on a 35mm camera would have an amazing 114mm aperture diameter. That requires a lot of glass, but it captures also a lot more photons for the same angle of view as the FZ50.
1) Angle of view a = 2 atan(I2 / 2F) which is approximately ( I2 / F) for I2 << 2F.
-- Introduction -- Lens & image -- A/D conversion -- Lumix & Leica -- Sharpness -- CCD noise1 -- CCD noise2 -- 5 years later --