|
|
 |
 |
 |
1.5 inch diameter tweeter in 3
inch and 6 x 6 inch baffles. The measurement microphone is at 24 inch distance and on the tweeter axis.
|
The impedance (1) of the tweeter shows a 3.2 kHz peak due to its mechanical resonance and a slight irregularity at 13 kHz. It can be expected that the frequency response rolls off at 12 dB/oct below the mechanical resonance as for any closed box dynamic driver.
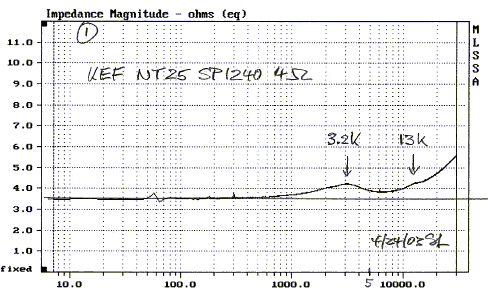
This roll-off behavior can be seen in the on-axis frequency response of the unbaffled driver (2). There is also a peak corresponding to the impedance irregularity at 13 kHz. The low frequency roll-off has no influence on the results of the following diffraction investigation since only the change in on-axis response due to the different baffles is of interest.
For a 3 inch circular baffle with a point source at its center there should be a 4.5 kHz peak, a 9 kHz dip, a 13,5 kHz peak, a 18 kHz dip and so on, whenever the edge is at multiples of a half wavelength from the source. Note that above about 14 kHz the baffle has no effect, because the dome has become too directional to illuminate the edge. The dome diameter becomes acoustically too large at higher frequencies to be considered a point source and the shape of the response ripples is smeared. Below 1000 Hz the baffle has decreasingly less effect. The source becomes omni-directional. With increasing frequency, though, the on-axis SPL of the 3" arrangement increases faster than for the bare tweeter. This is the so called "baffle step", where radiation contracts from 4p space to 2p space.
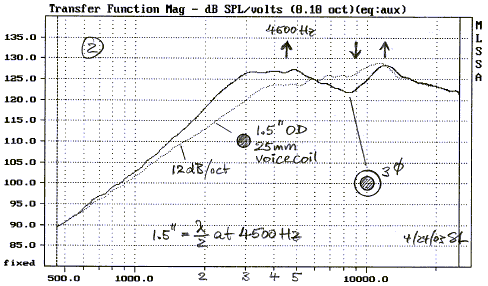
An increase in baffle diameter to 6" causes the baffle step to begin at half the frequency of the 3" baffle (3). The on-axis pressure increase due to diffraction can be up to 10 dB for a circular disc. This is approached at 2 kHz in (3) and at 1 kHz in (4) for the 12" disc. Note the increased number of peaks and dips as the baffle diameter is increased, and the peak to trough amplitude variation is not much different.
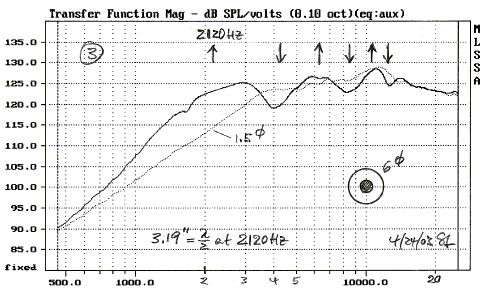
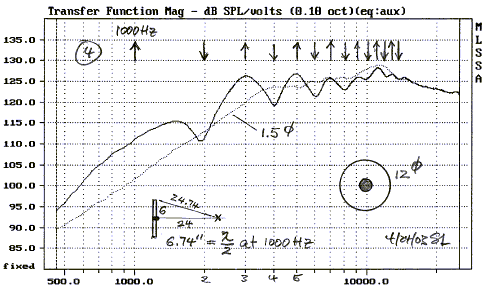
The diffraction ripple amplitude generally decreases with increasing frequency, because of increasing directivity of the driver and a sound pressure that is inversely proportional to the distance from the source to the edge (4).
The on-axis response for a thin circular baffle represents the worst case of diffraction. The typical rectangular baffle is more benign, because the distance from the tweeter to the edge varies and there are no frequencies for which all the distances are multiples of a half wavelength. A point source in the center of a square baffle is the worst case amongst rectangular baffles, because of symmetry.
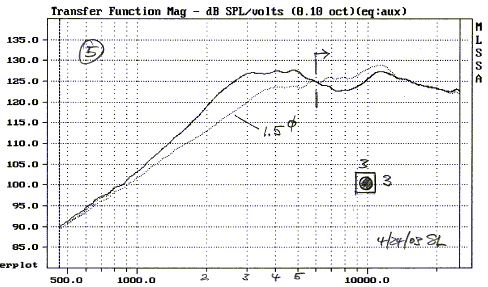
A small 3" square baffle gives only a slight reduction in diffraction ripple compared to a 3" disc (5, 2), because of the large dome size relative to the baffle. More effective is the 6" square baffle (6, 3). Note that above 6 kHz there is little difference in the response to a 3", 6" or 12" square baffle (5, 6, 7). The main differences are below this frequency.
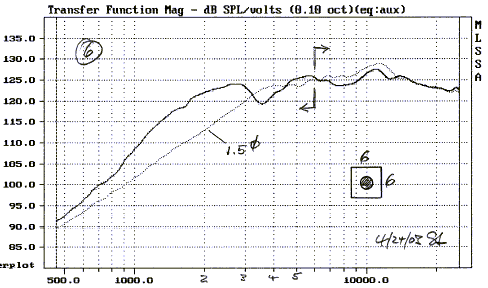
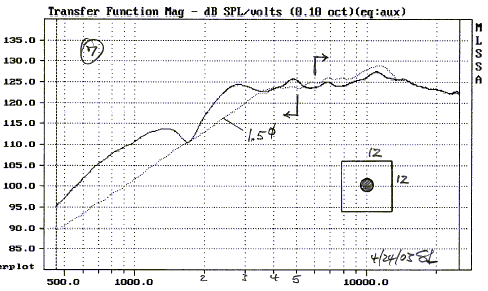
Reducing the width of the 12" square baffle to 6" has only effects below 5 kHz (7, 8).
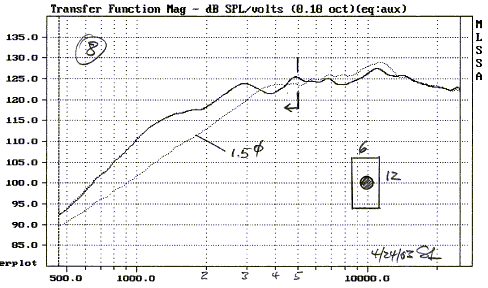
This even holds when the width is further reduced to 3" (7, 8, 9). The baffle step shifts up in frequency as the baffle becomes narrower, as would be expected.
I hope that the illustrations and FAQ 8 will give a little more insight into the complexities of diffraction and that it is difficult to speak in generalities about the effects of cabinet width, cabinet shape and driver diameter since they are wavelength dependent and change with frequency. It has been my experience that the on-axis and off-axis frequency response of a given driver and baffle combination must be measured to assess overall uniformity of response, and that computer models give pessimistic predictions, because the underlying assumptions do not sufficiently describe the real acoustic behavior of drivers and of cabinet shapes.
While I try to minimize visible diffraction ripples in the frequency response for good measure, I have no evidence that even strong diffraction effects have significant audible consequences, except for the transition region, the "baffle step", where radiation goes from omni-directional to forward firing. Note that there is no baffle step at 90 degrees off-axis, and boosting low frequencies for a flat on-axis response will add to the downward sloping trend of the frequency response off-axis. This causes a spectral imbalance of the reverberant sound field in the room and is a major reason why I prefer dipole radiators. Diffraction effects are always spatially localized and a slight shift in listening position will change their magnitude. While the "baffle step" cannot be avoided, the additional higher frequency ripples can be easily reduced to a magnitude that is much smaller than the first arriving direct sound, by simply optimizing the proportions of a rectangular baffle. The absolute width of a cabinet is not the critical parameter that many people think it is. Much is hypothesized, little is proven and much is overrated when it comes to diffraction.
| Diffraction | FAQ 38 |